How Your Trade Size Impacts Your Returns

Kelly’s Game Scenario

I go to a casino and walk over to the first table I see. The sign above the table says, “Kelly’s Game”. The dealer says, “Place a bet and The House will flip a coin. If you win the flip, The House will pay you 150% your money back. If you lose the bet, The House will keep 40% and return the remaining 60% to you.”

“That sounds great,” I say. Positive expected value. If I bet a lot, I should expect to get 105% of my money back on average. That’s a good bet. “What’s the catch?”

“Ah, yes. There is one more rule,” says the dealer. “You must bet all of the money you have each bet or not at all.”

The More Times I Bet, The Better I Should Do

How many times should I bet?

My intuition tells me that the more times I bet, the better I should do. The law of large numbers should mean that over time, my overall winnings per bet converge on my expected value of 105%.

In the long run, I feel like this is a rational bet. So, my strategy will be to make the bet 800 times and see where I am at. 

Since I’m betting all my money on each bet, I can only actually test my strategy once. Let’s think of that as a single universe, my universe, where we see a single unique chain of events.

But, before I actually go to the casino and bet it all, I want to guess what my universe will likely actually look like. To do that, we will simulate a multitude of universes, each completely independent of the others. 

Here’s 1,000 simulations of my strategy where each colored line is my total bank, each simulating a single possible universe where I execute the strategy faithfully:

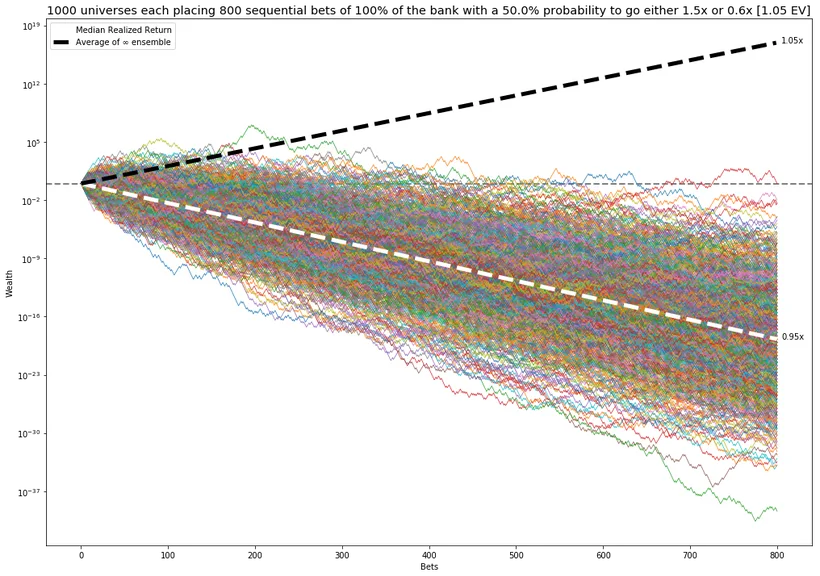
Notice the log Y scale. The dashed grey line with slope of 0 is breaking even. Negative slopes are losing money, and positive slopes are winning against The House.

The dotted black line is what I expected to gain, 105% per bet for 800 bets, netting me an expected 80,000,000,000,000 more than I started with. If I take the average of an infinite number of universes, my mean return is equal to the dotted black line.

The More Bets That I Make, The Worse It Gets

But I only sampled 1,000 universes. After 800 bets, only 1 universe in 1,000 has (just barely) more money than they started with. The more bets that I make, the worse it gets for me.

The typical (median) return marked by the dashed white line is 1,000,000,000,000,000,000 less than what I started with (since you can never reach 0, you always get 60% back). I have a few tiny fractions of a penny left and a dying dream to recoup my money.

The typical universe is very, very different than the average of all possible universes. I’m not from a mean universe. I’m from a typical, likely, universe. The median of a small number of samples more accurately reflects my reality than the mean of the infinite set.

While the total money in all universes grows at 105% per bet, the money leaks from the typical universes to just a few extremely rare, lottery winner universes. There are some small number of universes in the set where I win an ungodly amount of money, but in almost every other one I lose big.

Why is this so? In short, there are many more ways to lose money than to win money. Let’s look at all four of the possible universes of 2 sequential bets:

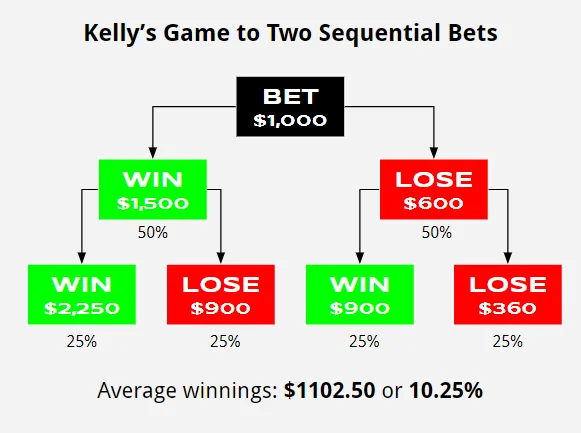
There Are More Ways To Lose Than Win

There is 1 way to win and 3 ways to lose. The average winnings are still 105% per bet, compounded to 110.25% over two bets, but 75% of the time you lose money and 25% of the time you win big.

The more times you bet, the worse it will typically get for you since you are more and more likely to be in one of the exponentially growing number of losing universes rather than the rare, exponentially rich ones.

In this game, the rational number of times to bet depends on how much you care about losing 40% or more of all of your money. Since I consider having a 50% chance to lose 40% of my money too unpalatable, the number of times it is rational for me to bet is zero, even though the bet is positive expected value.

Screw this game. In the universes where I bet 800 times I’ve lost all my money. In one of those universes, I go back home and wait for my next paycheck.

How To Win The Game

When my paycheck comes in, I go back to the casino and back to the same table with the same dealer. “Your game is rigged,” I say. “I want to bet against The House with my paycheck again, except this time I won’t bet everything I own every time. I want to bet less and see how it goes.” 

The dealer considers this, and says. “Fine. But you must pick a percentage and you must make every bet with that percentage of all of your money.”

“Great. I’ll bet half my money each time.” That way if I lose in the beginning, I’ll still have money to bet with. Let the gods simulate another 1,000 universes, using our new strategy:

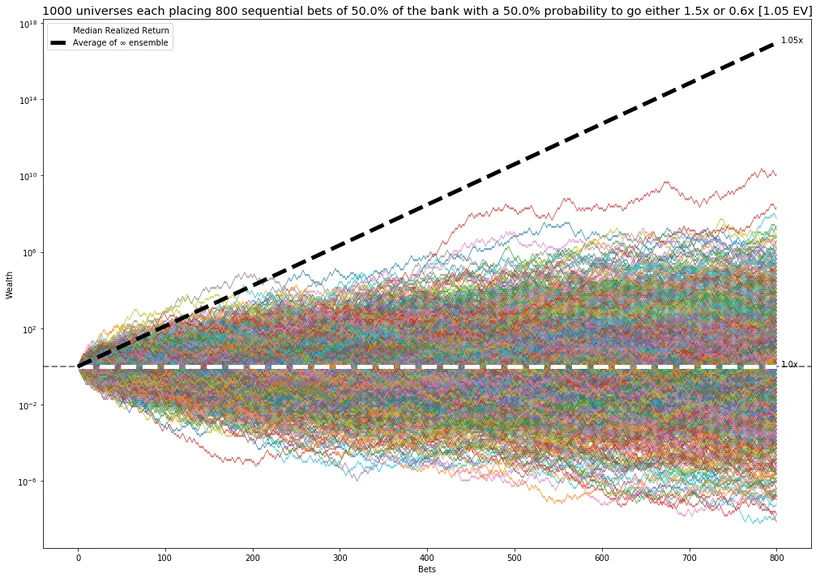
After 800 bets, half of our universes have made money, and half have lost money. Keep in mind that nothing has changed except how much of my total bank I use to bet. My typical universe is doing much better than before, but a far cry from the 80,000,000,000,000 return that my infinite selves are earning on average.

After 800 bets, I’m right back to where I started. The dealer says, “The House is feeling generous. You may now choose a new percentage to place on each bet. What will it be?”

Reducing my bet size improved my situation. Perhaps even smaller bets will continue to make things better. “Twenty five percent,” I declare as I lay down last week’s paycheck on the table, again. The gods flip the coin 800 times in 1,000 universes yet again:

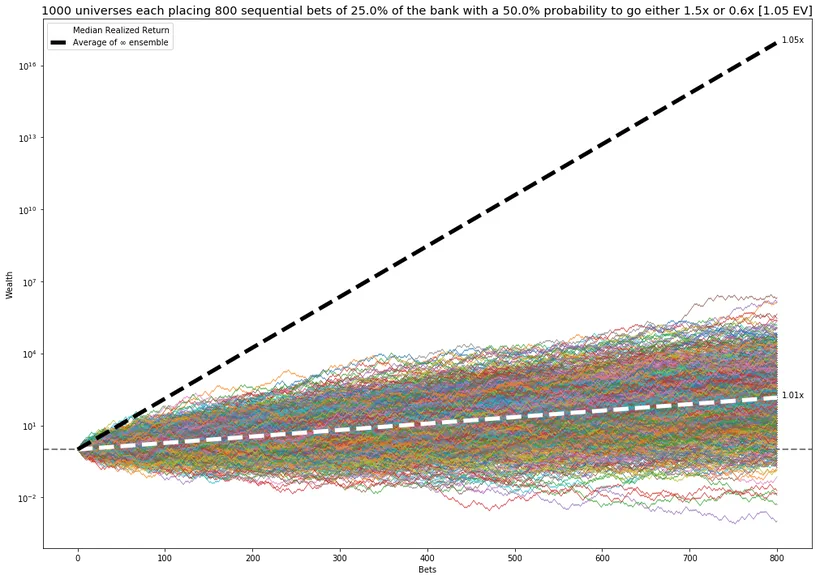
Now my typical universe is making good money, most of them are up more than 10x, and some as much as 100,000x. Now, satisfied, I finally get up to leave the casino with my money in my pocket. But, I have to know. I look at the dealer and ask, “So what’s the optimal bet?”

Kelly’s Criterion

In probability theory and intertemporal portfolio choice, the Kelly criterion (or Kelly strategy or Kelly bet), also known as the scientific gambling method, is a formula for bet sizing that leads almost surely to higher wealth compared to any other strategy in the long run (i.e. approaching the limit as the number of bets goes to infinity).

The Kelly bet size is found by maximizing the expected value of the logarithm of wealth, which is equivalent to maximizing the expected geometric growth rate. The Kelly Criterion is to bet a predetermined fraction of assets, and it can seem counterintuitive.

To calculate the optimal bet size use:

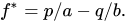
Kelly’s criterion where:

{b} is the the percent your investment increases by (from 1  to 1 + b)

{a} is the percent that your investment decreases by (from 1 to 1-a)

{p} is the probability of a win

{q=1-p} is the probability of a loss

{f*} is the fraction of the current bankroll to wager (i.e. how much to bet)

Using the calculator, you can see the the optimal bet size is 25% of your money on each bet:

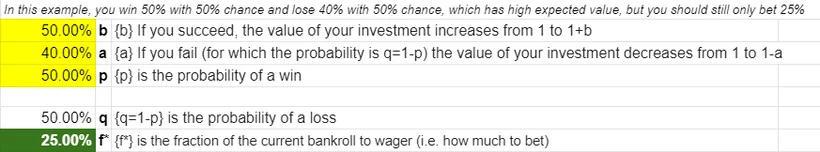
Looking again at the above graph, that means that the optimal betting strategy typically yields less than the expected value for the strategy.

Kelly’s Criterion Bet Size Calculator

Here’s a spreadsheet to play around with the above equation and calculate optimal bet sizes.  Make a copy and edit the cells highlighted in yellow to see what the optimal bet is. Read more in this awesome Nature Physics paper and this great article an AMMs.

This excellent work on position sizing was created by jamesj. If you liked this feature you can get nore useful trading info and strategies from you can also get more useful trading info like How To Trade Single Prints, Stockbee’s Trading Method,  Blackrock’s Aladdin, A Tutorial On Market Structure, How To Trade With the BPSPX, The ICT Candle Counting Method, How To Pass A Trader Evaluation & Get Funded, Five Trading Lessons I Learned From Citadel, The Top Step Trader Review, ICT Liquidity Runs, How To Trade The Options Chart & The Falang Futures Algo  and How To Use Volume To Trade Like Banks & Institutions